from fractions import Fraction
import numpy as np
import math
import matplotlib.pyplot as plt
from typing import *
import qiskit
from qiskit import QuantumCircuit, transpile
from qiskit_aer import AerSimulator
sim = AerSimulator()
from util import zero, one, qpe, qft_dagger, amod15, factor2_to_order
Shor’s Part 5/5: Shor’s Algorithm with Quantum Order Finding#
In this notebook, we’ll put together all the building blocks we have seen previously to implement Shor’s algorithm. Shor’s algorithm consists of
quantum order finding and
a continued fraction algorithm. We’ll focus on quantum order finding since it is the interesting quantum part of the algorithm.
References
Introduction to Classical and Quantum Computing, Chapter 7.7
Introduction to Quantum Information Science: Lectures 19 and 20 by Scott Aaronson
Quantum Computation and Quantum Information: Chapter 5, Nielsen and Chuang
Order Finding#
We’ll review classical order finding and probabilistic order finding to illustrate the difficulty of order finding with classical computation. We’ll then introduce quantum order finding.
Classical Order Finding#
Reminder: the goal is to find the order of a given \(a\) and \(N\), i.e., the smallest \(s\) such that
a = 7
N = 15
xs = [x for x in range(N)]
ys = [(a ** x) % N for x in xs]
plt.plot(xs, ys, marker="x")
plt.title("a=7 and N=15")
Text(0.5, 1.0, 'a=7 and N=15')
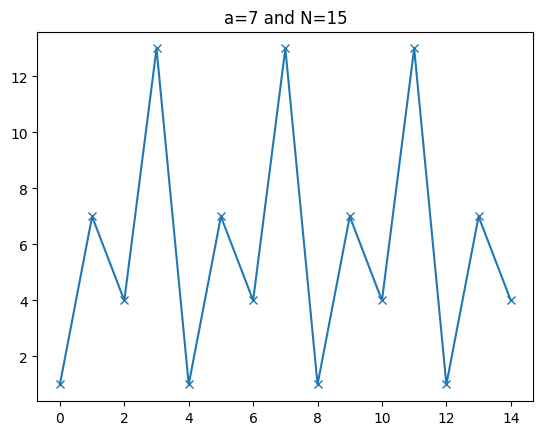
Deterministic algorithm#
We can just enumerate …
def order_find_det(a: int, N: int) -> int:
s = 1
while True:
if (a ** s) % N == 1:
return s
s += 1
order_find_det(7, 15)
4
Probabilistic Order Finding#
Let’s use the period finding formulation of order finding for \(a\) and \(N\) as \(f(x) = a^x \, (\text{mod} \, N)\).
Suppose we random sample numbers \(x\) and \(y\) and check if \(f(x) = f(y)\).
Since we have a periodic function with period \(s\), there are only \(s\) distinct values that \(f\) can take on.
How many \(x\)’s do we need to check before we find a collision?
Aside: Birthday paradox#
We require 23 people (\(\approx \sqrt{365}\)) before we find 2 people with the same birthday with probability at least 50%.
See https://en.wikipedia.org/wiki/Birthday_problem
count_collision = 0
for i in range(1000):
if len(np.unique(np.random.choice(np.arange(365), size=23))) != 23:
count_collision += 1
print("Probability of same birthday", count_collision/1000)
Probability of same birthday 0.511
Returning to Probabilistic algorithm#
Sample approximately \(\sqrt{s}\) to find a collision with probability 50%, i.e., an \(x\) and \(y\) such that \(f(x) = f(y)\).
Without loss of generality, assume that \(y > x\).
We know that \(s | y - x\) so that we can determine \(s\) with high probability if we find a few more collisions and compute the \(\text{gcd}(y_1 - x_1, y_2 - x_2, y_3 - x_3, \dots)\).
def order_find_prob(f: Callable, N: int, k: int = 4) -> int:
def go():
found = set()
found.add(f(0))
mapping = {f(0): 0}
while True:
x = np.random.choice(np.arange(N))
fx = f(x)
if fx in found:
return min(x, mapping[fx]), max(x, mapping[fx])
mapping[fx] = x
found.add(fx)
diffs = []
for i in range(k):
x, y = go()
diffs += [y - x]
return math.gcd(*diffs)
ans = []
for i in range(100):
ans += [order_find_prob(lambda x: (7 ** x) % 15, 15, k=4)]
plt.hist(ans)
(array([94., 0., 0., 0., 0., 0., 0., 0., 0., 6.]),
array([4. , 4.4, 4.8, 5.2, 5.6, 6. , 6.4, 6.8, 7.2, 7.6, 8. ]),
<BarContainer object of 10 artists>)
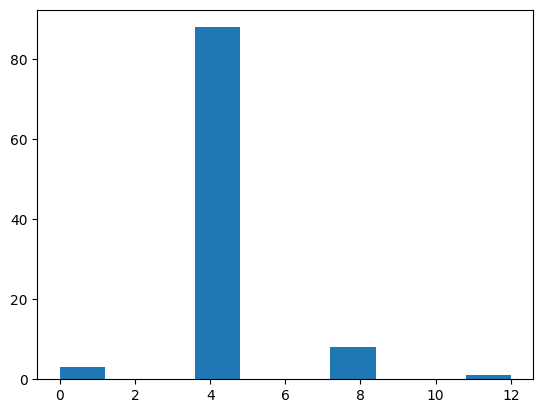
Analysis#
If \(s = 2^n\), then we require \(\sqrt{s} = 2^{n/2}\) queries.
For example, if \(n = 2056\), then we still require \(2^{1024}\) queries.
This is why RSA depends on large primes so that \(s\) is large.
In particular, since \(s | \phi(N)\) then either \(s | (p - 1)\) or \(s | (q - 1)\).
Quantum Order Finding#
The quantum order finding algorithm
uses QPE to estimate the phase of \(U\) and
followed by a continued fractions algorithm to extra the order from the phase.
Step 1: QPE#
def qpe_amodN(a: int, amodN: Callable, n_count: int) -> float:
# Construct circuit
qc = qpe(lambda q: amodN(a, q), n_count)
# Transplile away custom circuit
t_qc = transpile(qc, sim)
# Simulate
# Setting memory=True below allows us to see a list of each sequential reading
result = sim.run(t_qc, shots=1, memory=True).result()
readings = result.get_memory()
# Get phase
print("Register Reading: " + readings[0])
phase = int(readings[0],2)/(2**n_count)
print("Corresponding Phase: %f" % phase)
return phase
n_count = 8
N = 15
a = 7
phase = qpe_amodN(a, amod15, n_count)
phase
Register Reading: 00111000
Corresponding Phase: 0.218750
0.21875
Step 2: Continued Fractions Algorithm#
Fraction(phase).limit_denominator(N)
Fraction(2, 9)
Putting it together#
def order_find_quantum(a: int, N: int, amodN: Callable, n_count: int) -> int:
# Step 1: Perform QPE to get phase = \ell/s
phase = qpe_amodN(a, amodN, n_count)
# Step 2: Perform continued fractions algorithm to extract order
frac = Fraction(phase).limit_denominator(N) # Denominator should (hopefully!) tell us r
s = frac.denominator
return s
Shor’s Algorithm#
Apply quantum phase estimation to learn phase of \(U_f\).
Apply continued fractions algorithm to extract order from phase.
Apply factoring to order finding reduction.
def shors_algorithm(a: int, N: int, n_count: int) -> None:
attempt = 0
while True:
attempt += 1
print("\nAttempt %i:" % attempt)
# Step 1: Perform quantum order finding
if N == 15:
s = order_find_quantum(a, N, amod15, n_count)
else:
raise ValueError(f"Oracle not implemented for N = {N}")
print("Result: s = %i" % s)
# Step 2: Solve factor in terms of order finding
if phase != 0:
maybe_guess = factor2_to_order(N, a, s)
if maybe_guess is not None:
print("*** Non-trivial factor found: %i ***" % maybe_guess)
break
n_count = 8
N = 15
a = 7
shors_algorithm(a, N, n_count)
Attempt 1:
Register Reading: 11011000
Corresponding Phase: 0.843750
Result: s = 13
13
Attempt 2:
Register Reading: 10000100
Corresponding Phase: 0.515625
Result: s = 2
*** Non-trivial factor found: 3 ***