from typing import *
import math
import matplotlib.pyplot as plt

Appendix: Factoring Integers

In this notebook, we’ll cover the basics of factoring integers at the level needed to understand RSA and Shor’s algorithm. This includes reviewing

1. basic number theory,

2. the order finding problem,

3. and reducing factoring to order finding.

Basic Number Theory

Prime Numbers

A number \(p\) is prime if it cannot be divided by any other number except \(1\) and \(p\).

def prime_seive(n):
    def seive(primes, i):
        for prime in primes:
            if prime > math.ceil(math.sqrt(n)):
                break
            if i % prime == 0:
                return False
        return True
    
    primes = [2, 3, 5]
    for i in range(6, n, 6):
        if seive(primes, i - 1):
            primes += [i - 1]
        if seive(primes, i + 1):
            primes += [i + 1]
    return primes

prime_seive(50)

[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47]

Prime Factorization

Every number \(n\) has a prime factorization, i.e.,

\[ n = p_1 \dots p_m \]

where \(p_i\) is a prime.

def factor(n):
    factors = []
    primes = prime_seive(n)
    for prime in primes:
        while n % prime == 0:
            factors += [prime]
            n = n / prime
        if prime > n:
            break
    return factors

factor(2 * 73 * 2 * 5 * 3  * 89)

[2, 2, 3, 5, 73, 89]

factor(123412), 2 * 2 * 30853

([2, 2, 30853], 123412)

Remainder, Divisibility, Modulus

1. Every positive integer can be written as

\[ x = nm + r \]

for some choice of \(n, m, r\). 2. We say that \(x\) is congruent to \(r\) mod \(m\), written

\[ x \equiv r \, (\text{mod} \, m) \]

when \(x = nm + r\). Note that \(\equiv\) is an equivalence relation.

3. We say that \(m\) divides \(x\), written

\[ m | x \]

if \(r = 0\) or equivalently \(x \equiv 0 \, (\text{mod} \, m)\).

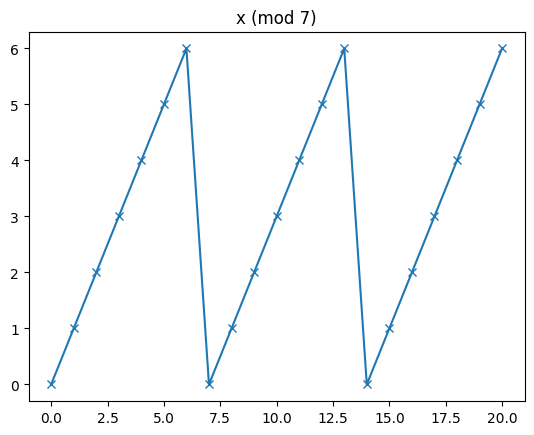
xs = [x for x in range (21)]
ys = [x % 7 for x in range(21)] # x (mod 7)
plt.plot(xs, ys, marker='x')
plt.title('x (mod 7)')

Text(0.5, 1.0, 'x (mod 7)')

Greatest Common Divisor

1. The greatest common divisor (gcd) of two numbers \(n\) and \(m\), written \(\text{gcd}(n, m)\), is the largest number \(k\) such that \(k | n\) and \(k | m\).

2. The gcd can be computed in polynomial time.

3. Two numbers \(n\) and \(m\) are relatively prime if \(\text{gcd}(n, m) = 1\).

math.gcd(10, 20)

10

math.gcd(3, 5)  # 3 and 5 are relatively prime

1

math.gcd(10, 21)  # 10 and 21 are relatively prime, but neither are prime

1

Fermat’s little theorem

Fermat’s little theorem states that

\[ x^{p-1} \equiv 1 \, (\text{mod} \, p) \]

for any prime \(p\) and \(1 \leq x \leq p - 1\).

# Example: Fermat's little theorem
x = 2; p = 7
acc = [x]
for i in range(2, 7):
    acc += [(acc[-1] * x) % p]
acc  # contains x^i (mod p) for 1 <= i <= p - 1

[2, 4, 1, 2, 4, 1]

Observation

Multiplication of numbers \(\{ 1, \dots, p-1 \}\) mod \(p\) is a permutation.

p = 7
print(f"Multiplication (mod {p})")
print("x\\y ", " ".join([str(y) for y in range(1, p)]))
for x in range(1, p):
    print(' ', x, [(x * y) % p for y in range(1, p)])

Multiplication (mod 7)
x\y  1 2 3 4 5 6
  1 [1, 2, 3, 4, 5, 6]
  2 [2, 4, 6, 1, 3, 5]
  3 [3, 6, 2, 5, 1, 4]
  4 [4, 1, 5, 2, 6, 3]
  5 [5, 3, 1, 6, 4, 2]
  6 [6, 5, 4, 3, 2, 1]

Euler’s totient function

Euler’s totient function

\[ \phi(N) = |\{ n : \text{gcd}(n, x) = 1, n \in \mathbb{N} \}| \]

gives the number of naturals less than \(N\) that are relatively prime to \(N\).

def euler_totient(N):
    cnt = 0
    for i in range(N):
        if math.gcd(i, N) == 1:
           cnt += 1
    return cnt

euler_totient(9)

6

euler_totient(11*13), 10 * 12

(120, 120)

Euler’s theorem

Euler’s theorem states that

\[ x^{(p-1)(q-1)} \equiv 1 \, (\text{mod} \, pq) \]

for any distinct primes \(p, q\) and \(1 \leq x \leq (p - 1)(q - 1)\).

# Example: Euler's theorem
x = 2; p = 3; q = 5
acc = [x]
for i in range(2, (p-1)*(q-1)+1):
    acc += [(acc[-1] * x) % (p*q)]
acc  # contains x^i (mod p) for 1 <= i <= (p - 1)(q - 1)

[2, 4, 8, 1, 2, 4, 8, 1]

Order Finding Problem

1. Let \(a < N\) be relatively prime.

2. The order of \(a\) is the smallest number \(s\) such that

\[ a^s \equiv 1 \, (\text{mod} \, N) \]

3. The order finding problem is to determine the order of some given \(a\) and \(N\).

Example

Here is an example where we choose \(a = 3\) and \(N = 35\).

xs = [i for i in range(35)]
ys = [(3 ** x) % 35 for x in xs]
plt.plot(xs, ys, marker='x', linestyle='--')
plt.title("a=3 and N = 35")

Text(0.5, 1.0, 'a=3 and N = 35')

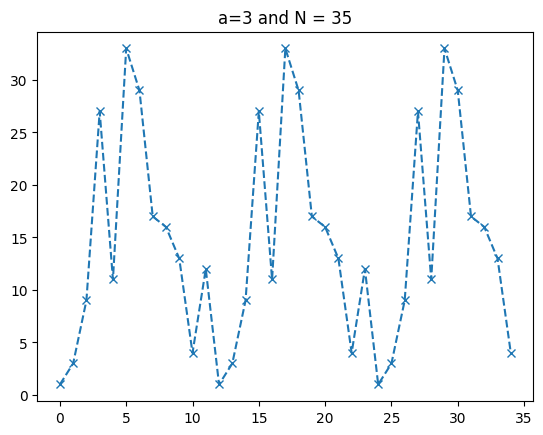
# order is 12

Aside: Period finding

A function \(f: \mathbb{N} \rightarrow \mathbb{N}\) is periodic if there is period \(s > 0\) such that

\[ f(x) = f(y) \iff s | (y - x) \]

for every \(x\) and \(y\).

1. \(s | (y - x)\) is notation for \(s\) divides \(y - x\).

2. The period finding problem is to determine the period \(s\) given oracle access to \(f\).

3. The period finding problem is a generalization of the order finding problem.

Reducing Factoring to Order Finding

1. We don’t need to solve the general case of factoring an arbitrary number.

2. Instead, we’ll just focus on factoring a product of two primes, which is the setting of Shor’s algorithm.

Reducing factoring to order finding

Suppose we are trying to factor \(N = pq\) for primes \(p\) and \(q\).

1. Pick a random r relatively prime to \(N\) (which happens unless r is p or q).

2. Find the order \(s\) of

\[ r^x \, (\text{mod} \, N) \,. \]

• This means that \(r^s \equiv 1 \, (\text{mod} \, N)\) since \(r^0 \equiv 1 \, (\text{mod} \, N)\).

  • Use a order finding algorithm to find s. We’ll leave as a blackbox since we are reducing factoring to order finding.

3. Suppose \(s\) is even. Then \begin{align} 0 , (\text{mod} , N) & = r^{s} - 1 \tag{definition of order} \ & = (r^{s/2} - 1)(r^{s/2} + 1) \tag{Factoring} \end{align}

   • Recall \(r^{\phi(N)} \equiv 1 \, (\text{mod} \, N)\) by Euler’s theorem.

   • Thus \(s | \phi(N)\).

4. Suppose further that neither \((r^{s/2} - 1)\) nor \((r^{s/2} + 1)\) is a multiple of \(N\). Then either \(\text{gcd}(r^{s/2} - 1, N)\) or \(\text{gcd}(r^{s/2} + 1, N)\) is a factor of \(N\), which gives us \(p\) and subsequently \(q\).

5. If either condition 3 or 4 fail, goto 1. The probability that steps 3 and 4 succeed is greater than \(1/2\). See Neilsen and Chuang Theorem A4.13.

Example

Factor \(N = 3 \cdot 5\).

N = 35   # number we are trying to factor

# Step 1
r = 17    # randomly choosen

# Step 2: Order find somehow
xs = [x for x in range(15)]
ys = [(r ** x) % N for x in xs]
plt.plot(xs, ys, marker='x')

[<matplotlib.lines.Line2D at 0x7f3080403980>]

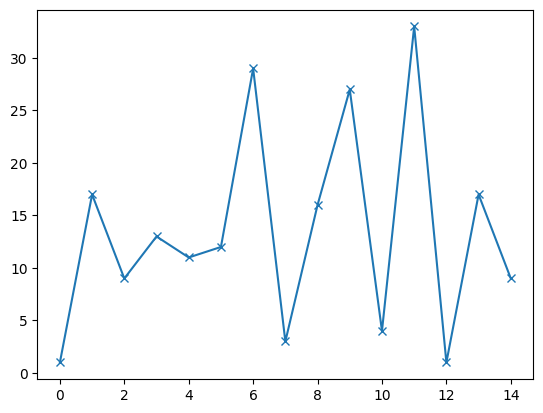
# Step 3: order find somehow
s = 12 # manual inspection
# s is even, so we can continue
left, right = int(r ** (s / 2) - 1), int(r ** (s / 2) + 1)
left, right

(24137568, 24137570)

# Step 4: Check the multiple condition
print("Left multiple of N", left % N == 0)
print("Right multiple of N", right % N == 0)
math.gcd(left, N), math.gcd(right, N)

Left multiple of N False
Right multiple of N False

(7, 5)

# Step 5: return the primes
math.gcd(left, N), N / math.gcd(left, N)

(7, 5.0)

Putting it together

We can put the steps above together into an algorithm that reduces factoring to order finding.

def factor2_to_order(N: int, a: int, s: int) -> int:
    # Check that s is even
    if s % 2 != 0:
        print(s)
        return None
    
    guesses = [math.gcd(a**(s//2)-1, N), math.gcd(a**(s//2)+1, N)]
    for guess in guesses:
        # Check to see if guess is a factor
        if guess not in [1, N] and (N % guess) == 0:
            return guess